How Does The Simulator Work?

Background

This simulator is a work-in-progress and based on the thesis report "Modelling Speargun Dynamics" currently being completed for the award of an Msc in Gun Systems Design at Cranfield University. Development is not expected to finalise before Q1 2021 due to COVID-19 delays. The capabilities and limitations of this preliminary model are discussed below:

Determining Energy

27 rubber samples were tested and their forces at various percentage elongations recorded. An average force vs. elongation % function was developed for each diameter, the 16mm function is pictured below:

The black dots represent experimental data points, the blue area is energy dissipated by the rubber after 30 minutes of tension and the orange area is the energy released by the rubber.

The rubber data was derived by letting the samples dissipate for 30 minutes prior to recording the energy released, during which time approximately 30% of the input energy was dissipated. The simulator will not mirror actual performance if the gun isn’t loaded for exactly 30 minutes before firing. If the gun is fired after 30 minutes, the shaft performance will be lower as more energy will have dissipated from the rubber. If the shaft is fired before 30 minutes has elapsed, the system energy will be higher. It may even be higher than the frictional losses, in which case reality would outperform the simulator.

Further information regarding how the energy data is handled can be downloaded here (link).

Calculating Results

A number of equations were derived that model the dynamic behavior of conventional, roller and inverted spearguns. These equations assume free recoil and haven't yet been corrected for hydrodynamic frictional losses. The incorporation of frictional losses requires further testing which will be conducted in Q4 2020. The simulator server uses the general programming language Python to solve systems of these equations, an example of which is pictured below:

More information regarding how these equations were derived can be downloaded here (link).

Shaft Buckling

Shaft buckling is when the shaft flexes during firing and is detrimental to accuracy. Buckling occurs when the shooting force applied to the shaft is too great. Buckling is dependant on the shaft length, thickness, load applied and how the shaft is supported. The simulator divides the culminative rubber forces for each speargun configuration by Euler's critical load for buckling (pictured below) to determine a buckling propensity.

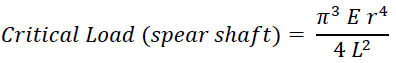
The simulator cannot determine whether a speargun configuration will experience buckling or not; there are still too many additional unknown variables. However, it is able to calculate and compare the buckling resistance of two different speargun configurations.

Hydrodynamic Drag

Hydrodynamic drag deccelerates the spear after it is fired; the spear velocity decreases the further a spear travels. The simulator assumes a spear shaft drag coefficient of 0.82 to determine how fast the shaft is moving using the equation below:

The equation is re-evaluated every millimetre of the shaft's travel, or 8,000 times over an 8 metre range, to account for changing acceleration. The assumed drag coefficient is an interim measure until one can be experimentally derived in Q4 2020. More information regarding the derivation of the drag formula can be downloaded here (link).

Penetration

Penetration takes the shaft velocity at specific ranges as well as other shaft parameters and predicts a penetration depth using an equation for low-speed non-deformable projectiles penetrating a compression-failing thick medium:

Is assumes the fish tissue cavity strength is approximately 20 Megapascals (similiar to human tissue) but the cavity strength must be experimentally determined in Q4 2020.

Shaft bending

A shaft can bend when the diver is attempting to haul a fish to the surface. The simulator compares the bending resistance of two spear shafts using the stress formula for a fixed-free cantilever round rod:

Like buckling, there are too many unknown variables to determine if a shaft will bend, however the simulator can compare the bending resistance of two shafts.

Current Limitations & Assumptions Summary

Rubber Data. Rubber dissipates energy if left stretched over time; the simulator assumes the gun remains loaded for 30 mins before firing.
Equations of Motion. The simulator assumes (unheld) free recoil; the shaft velocity is likely to be higher if the speargun is held firmly.
Hydrodynamic Friction. The simulator does not yet account for friction.
Drag Coefficient. The simulator assumes a drag coefficient of 0.82.
Buckling and Bending. The simulator can only compare buckling and bending resilience, not predict it's occurrence.
Penetration. The simulator assumes fish cavity strength of 20 Mpa.

Testing to determine friction losses, a shaft drag coefficient and the cavity strength of fish issue is scheduled for Q4 2020.